Quantum key distribution
Quantum key distribution (QKD) uses quantum mechanics to guarantee secure communication. It enables two parties to produce a shared random secret key known only to them, which can then be used to encrypt and decrypt messages. It is often incorrectly called quantum cryptography, as it is the most well known example of the group of quantum cryptographic tasks.
An important and unique property of quantum distribution is the ability of the two communicating users to detect the presence of any third party trying to gain knowledge of the key. This results from a fundamental aspect of quantum mechanics: the process of measuring a quantum system in general disturbs the system. A third party trying to eavesdrop on the key must in some way measure it, thus introducing detectable anomalies. By using quantum superpositions or quantum entanglement and transmitting information in quantum states, a communication system can be implemented which detects eavesdropping. If the level of eavesdropping is below a certain threshold, a key can be produced that is guaranteed to be secure (i.e. the eavesdropper has no information about), otherwise no secure key is possible and communication is aborted.
The security of quantum key distribution relies on the foundations of quantum mechanics, in contrast to traditional key distribution protocol which relies on the computational difficulty of certain mathematical functions, and cannot provide any indication of eavesdropping or guarantee of key security.
Quantum key distribution is only used to produce and distribute a key, not to transmit any message data. This key can then be used with any chosen encryption algorithm to encrypt (and decrypt) a message, which can then be transmitted over a standard communication channel. The algorithm most commonly associated with QKD is the one-time pad, as it is provably secure when used with a secret, random key.[1]
Contents |
Quantum key exchange
Quantum communication involves encoding information in quantum states, or qubits, as opposed to classical communication's use of bits. Usually, photons are used for these quantum states. Quantum key distribution exploits certain properties of these quantum states to ensure its security. There are several different approaches to quantum key distribution, but they can be divided into two main categories depending on which property they exploit.
- Prepare and measure protocols
- In contrast to classical physics, the act of measurement is an integral part of quantum mechanics. In general, measuring an unknown quantum state changes that state in some way. This is known as quantum indeterminacy, and underlies results such as the Heisenberg uncertainty principle, information-disturbance theorem and no cloning theorem. This can be exploited in order to detect any eavesdropping on communication (which necessarily involves measurement) and, more importantly, to calculate the amount of information that has been intercepted.
- Entanglement based protocols
- The quantum states of two (or more) separate objects can become linked together in such a way that they must be described by a combined quantum state, not as individual objects. This is known as entanglement and means that, for example, performing a measurement on one object affects the other. If an entangled pair of objects is shared between two parties, anyone intercepting either object alters the overall system, revealing the presence of the third party (and the amount of information they have gained).
These two approaches can each be further divided into three families of protocols; discrete variable, continuous variable and distributed phase reference coding. Discrete variable protocols were the first to be invented, and they remain the most widely implemented. The other two families are mainly concerned with overcoming practical limitations of experiments. The two protocols described below both use discrete variable coding.
BB84 protocol: Charles H. Bennett and Gilles Brassard (1984)
This protocol, known as BB84 after its inventors and year of publication, was originally described using photon polarization states to transmit the information. However, any two pairs of conjugate states can be used for the protocol, and many optical fibre based implementations described as BB84 use phase encoded states. The sender (traditionally referred to as Alice) and the receiver (Bob) are connected by a quantum communication channel which allows quantum states to be transmitted. In the case of photons this channel is generally either an optical fibre or simply free space. In addition they communicate via a public classical channel, for example using broadcast radio or the internet. Neither of these channels need to be secure; the protocol is designed with the assumption that an eavesdropper (referred to as Eve) can interfere in any way with both.
The security of the protocol comes from encoding the information in non-orthogonal states. Quantum indeterminacy means that these states cannot in general be measured without disturbing the original state (see No cloning theorem). BB84 uses two pairs of states, with each pair conjugate to the other pair, and the two states within a pair orthogonal to each other. Pairs of orthogonal states are referred to as a basis. The usual polarization state pairs used are either the rectilinear basis of vertical (0°) and horizontal (90°), the diagonal basis of 45° and 135° or the circular basis of left- and right-handedness. Any two of these bases are conjugate to each other, and so any two can be used in the protocol. Below the rectilinear and diagonal bases are used.
| Basis | 0 | 1 |
|---|---|---|
The first step in BB84 is quantum transmission. Alice creates a random bit (0 or 1) and then randomly selects one of her two bases (rectilinear or diagonal in this case) to transmit it in. She then prepares a photon polarization state depending both on the bit value and basis, as shown in the table to the left. So for example a 0 is encoded in the rectilinear basis (+) as a vertical polarization state, and a 1 is encoded in the diagonal basis (x) as a 135° state. Alice then transmits a single photon in the state specified to Bob, using the quantum channel. This process is then repeated from the random bit stage, with Alice recording the state, basis and time of each photon sent.
According to quantum mechanics (particularly quantum indeterminacy), no possible measurement distinguishes between the 4 different polarization states, as they are not all orthogonal. The only possible measurement is between any two orthogonal states (a basis). So, for example, measuring in the rectilinear basis gives a result of horizontal or vertical. If the photon was created as horizontal or vertical (as a rectilinear eigenstate) then this measures the correct state, but if it was created as 45° or 135° (diagonal eigenstates) then the rectilinear measurement instead returns either horizontal or vertical at random. Furthermore, after this measurement the photon is polarized in the state it was measured in (horizontal or vertical), with all information about its initial polarization lost.
As Bob does not know the basis the photons were encoded in, all he can do is to select a basis at random to measure in, either rectilinear or diagonal. He does this for each photon he receives, recording the time, measurement basis used and measurement result. After Bob has measured all the photons, he communicates with Alice over the public classical channel. Alice broadcasts the basis each photon was sent in, and Bob the basis each was measured in. They both discard photon measurements (bits) where Bob used a different basis, which is half on average, leaving half the bits as a shared key.
| Alice's random bit | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|
| Alice's random sending basis | ||||||||
| Photon polarization Alice sends | ||||||||
| Bob's random measuring basis | ||||||||
| Photon polarization Bob measures | ||||||||
| PUBLIC DISCUSSION OF BASIS | ||||||||
| Shared secret key | 0 | 1 | 0 | 1 | ||||
To check for the presence of eavesdropping Alice and Bob now compare a certain subset of their remaining bit strings. If a third party (usually referred to as Eve, for 'eavesdropper') has gained any information about the photons' polarization, this introduces errors in Bobs' measurements. If more than  bits differ they abort the key and try again, possibly with a different quantum channel, as the security of the key cannot be guaranteed.
bits differ they abort the key and try again, possibly with a different quantum channel, as the security of the key cannot be guaranteed.  is chosen so that if the number of bits known to Eve is less than this, privacy amplification can be used to reduce Eve's knowledge of the key to an arbitrarily small amount, by reducing the length of the key.
is chosen so that if the number of bits known to Eve is less than this, privacy amplification can be used to reduce Eve's knowledge of the key to an arbitrarily small amount, by reducing the length of the key.
E91 protocol: Artur Ekert (1991)
The Ekert scheme uses entangled pairs of photons. These can be created by Alice, by Bob, or by some source separate from both of them, including eavesdropper Eve. The photons are distributed so that Alice and Bob each end up with one photon from each pair.
The scheme relies on two properties of entanglement. First, the entangled states are perfectly correlated in the sense that if Alice and Bob both measure whether their particles have vertical or horizontal polarizations, they always get the same answer with 100% probability. The same is true if they both measure any other pair of complementary (orthogonal) polarizations. However, the particular results are completely random; it is impossible for Alice to predict if she (and thus Bob) will get vertical polarization or horizontal polarization. Second, any attempt at eavesdropping by Eve destroys these correlations in a way that Alice and Bob can detect. The original Ekert protocol consist of using three possible states and testing Bell inequality violation for detecting eavesdropping.
Privacy amplification and information reconciliation
The quantum key distribution protocols described above provide Alice and Bob with nearly identical shared keys, and also with an estimate of the discrepancy between the keys. These differences can be caused by eavesdropping, but also by imperfections in the transmission line and detectors. As it is impossible to distinguish between these two types of errors, guaranteed security requires the assumption that all errors are due to eavesdropping. Provided the error rate between the keys is lower than a certain threshold (20% as of April 2007[2]), two steps can be performed to first remove the erroneous bits and then reduce Eve's knowledge of the key to an arbitrary small value. These two steps are known as information reconciliation and privacy amplification respectively, and were first described in 1992.[3]
Information reconciliation is a form of error correction carried out between Alice and Bob's keys, in order to ensure both keys are identical. It is conducted over the public channel and as such it is vital to minimise the information sent about each key, as this can be read by Eve. A common protocol used for information reconciliation is the cascade protocol, proposed in 1994.[4] This operates in several rounds, with both keys divided into blocks in each round and the parity of those blocks compared. If a difference in parity is found then a binary search is performed to find and correct the error. If an error is found in a block from a previous round that had correct parity then another error must be contained in that block; this error is found and corrected as before. This process is repeated recursively, which is the source of the cascade name. After all blocks have been compared, Alice and Bob both reorder their keys in the same random way, and a new round begins. At the end of multiple rounds Alice and Bob have identical keys with high probability, however Eve has additional information about the key from the parity information exchanged.
Privacy Amplification is a method for reducing (and effectively eliminating) Eve's partial information about Alice and Bob's key. This partial information could have been gained both by eavesdropping on the quantum channel during key transmission (thus introducing detectable errors), and on the public channel during information reconciliation (where it is assumed Eve gains all possible parity information). Privacy amplification uses Alice and Bob's key to produce a new, shorter key, in such a way that Eve has only negligible information about the new key. This can be done using a universal hash function, chosen at random from a publicly known set of such functions, which takes as its input a binary string of length equal to the key and outputs a binary string of a chosen shorter length. The amount by which this new key is shortened is calculated, based on how much information Eve could have gained about the old key (which is known due to the errors this would introduce), in order to reduce the probability of Eve having any knowledge of the new key to a very low value.
Implementations
Experimental
The highest bit rate system currently demonstrated exchanges secure keys at 1 Mbit/s (over 20 km of optical fibre) and 10 kbit/s (over 100 km of fibre), achieved by a collaboration between the University of Cambridge and Toshiba using the BB84 protocol with decoy pulses.[5]
As of March 2007[update] the longest distance over which quantum key distribution has been demonstrated using optic fibre is 148.7 km, achieved by Los Alamos National Laboratory/NIST using the BB84 protocol.[6] Significantly, this distance is long enough for almost all the spans found in today's fibre networks. The distance record for free space QKD is 144 km between two of the Canary Islands, achieved by a European collaboration using entangled photons (the Ekert scheme) in 2006,[7] and using BB84 enhanced with decoy states[8] in 2007.[9] The experiments suggest transmission to satellites is possible, due to the lower atmospheric density at higher altitudes. For example although the minimum distance from the International Space Station to the ESA Space Debris Telescope is about 400 km, the atmospheric thickness is about an order of magnitude less than in the European experiment, thus yielding less attenuation compared to this experiment.
Commercial
There are currently four companies offering commercial quantum key distribution systems; id Quantique (Geneva), MagiQ Technologies (New York), SmartQuantum (France) and Quintessence Labs (Australia). Several other companies also have active research programmes, including Toshiba, HP, IBM, Mitsubishi, NEC and NTT (See External links for direct research links).
Quantum encryption technology provided by the Swiss company Id Quantique was used in the Swiss canton (state) of Geneva to transmit ballot results to the capitol in the national election occurring on October 21, 2007.[10]
In 2004, the world's first bank transfer using quantum key distribution was carried in Vienna, Austria. An important cheque, which needed absolute security, was transmitted from the Mayor of the city to an Austrian bank.[11]
Quantum Key Distribution Networks
DARPA
The DARPA Quantum network,[12] a 10-node quantum key distribution network, has been running since 2004 in Massachusetts, USA. It is being developed by BBN Technologies, Harvard University, Boston University and QinetiQ.
SECOQC
The world's first computer network protected by quantum key distribution was implemented in October 2008, at a scientific conference in Vienna. The name of this network is SECOQC (Secure Communication Based on Quantum Cryptography) and EU funded this project. The network used 200 km of standard fibre optic cable to interconnect six locations across Vienna and the town of St Poelten located 69 km to the west.[13]
SwissQuantum
Id Quantique SA announced the successful completion of the longest running project for testing Quantum Key Distribution (QKD) in a field environment. The main goal of the SwissQuantum network [14], installed in the Geneva metropolitan area in March 2009, was to validate the reliability and robustness of QKD in continuous operation over a long time period in a field environment. The quantum layer ran stably for nearly 2 years until the completion of the project in January 2011, confirming the viability of QKD as a commercial encryption technology.
Tokyo QKD Network
The Tokyo QKD Network[15] was inaugurated on the first day of the UQCC2010 conference. The network involves an international collaboration between 7 partners; NEC, Mitsubishi Electric, NTT and NICT from Japan, and participation from Europe by Toshiba Research Europe Ltd. (UK), Id Quantique (Switzerland) and All Vienna (Austria). "All Vienna" is represented by researchers from the Austrian Institute of Technology (AIT), the Institute for Quantum Optics and Quantum Information (IQOQI) and the University of Vienna.
Attacks
Example: Intercept and resend
The simplest type of possible attack is the intercept-resend attack, where Eve measures the quantum states (photons) sent by Alice and then sends replacement states to Bob, prepared in the state she measures. In the BB84 protocol, this produces errors in the key Alice and Bob share. As Eve has no knowledge of the basis a state sent by Alice is encoded in, she can only guess which basis to measure in, in the same way as Bob. If she chooses correctly, she measures the correct photon polarization state as sent by Alice, and resends the correct state to Bob. However, if she chooses incorrectly, the state she measures is random, and the state sent to Bob cannot be the same as the state sent by Alice. If Bob then measures this state in the same basis Alice sent, he too gets a random result—as Eve has sent him a state in the opposite basis— with a 50% chance of an erroneous result (instead of the correct result he would get without the presence of Eve). The table below shows an example of this type of attack.
| Alice's random bit | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|
| Alice's random sending basis | ||||||||
| Photon polarization Alice sends | ||||||||
| Eve's random measuring basis | ||||||||
| Polarization Eve measures and sends | ||||||||
| Bob's random measuring basis | ||||||||
| Photon polarization Bob measures | ||||||||
| PUBLIC DISCUSSION OF BASIS | ||||||||
| Shared secret key | 0 | 0 | 0 | 1 | ||||
| Errors in key | ✓ | ✘ | ✓ | ✓ | ||||
The probability Eve chooses the incorrect basis is 50% (assuming Alice chooses randomly), and if Bob measures this intercepted photon in the basis Alice sent he gets a random result, i.e., an incorrect result with probability of 50%. The probability an intercepted photon generates an error in the key string is then 50% × 50% = 25%. If Alice and Bob publicly compare  of their key bits (thus discarding them as key bits, as they are no longer secret) the probability they find disagreement and identify the presence of Eve is
of their key bits (thus discarding them as key bits, as they are no longer secret) the probability they find disagreement and identify the presence of Eve is
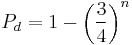
So to detect an eavesdropper with probability 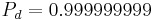 Alice and Bob need to compare
Alice and Bob need to compare 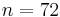 key bits.
key bits.
Security Proofs
The above is just a simple example of an attack. If Eve is assumed to have unlimited resources, for example classical and quantum computing power, there are many more attacks possible. BB84 has been proven secure against any attacks allowed by quantum mechanics, both for sending information using an ideal photon source which only ever emits a single photon at a time,[16] and also using practical photon sources which sometimes emit multiphoton pulses.[17] These proofs are unconditionally secure in the sense that no conditions are imposed on the resources available to the Eavesdropper, however there are other conditions required:
- Eve cannot access Alice and Bob's encoding and decoding devices.
- The random number generators used by Alice and Bob must be trusted and truly random (for example a Quantum random number generator).
- The classical communication channel must be authenticated using an unconditionally secure authentication scheme.
- The message must be sent encrypted by correctly used one-time pad (unconditionally secure encryption) scheme.
Man-in-the-middle attack
Quantum key distribution is vulnerable to a man-in-the-middle attack when used without authentication to the same extent as any classical protocol, since no known principle of quantum mechanics can distinguish friend from foe. As in the classical case, Alice and Bob cannot authenticate each other and establish a secure connection without some means of verifying each other's identities (such as an initial shared secret). If Alice and Bob have an initial shared secret then they can use an unconditionally secure authentication scheme (such as Carter-Wegman,[18]) along with quantum key distribution to exponentially expand this key, using a small amount of the new key to authenticate the next session.[19] Several methods to create this initial shared secret have been proposed, for example using a 3rd party[20] or chaos theory.[21] Nevertheless only "almost strongly universal" family of hash functions can be used for unconditionally secure authentication.[22]
Photon number splitting attack
In the BB84 protocol Alice sends quantum states to Bob using single photons. In practice many implementations use laser pulses attenuated to a very low level to send the quantum states. These laser pulses contain a very small number of photons, for example 0.2 photons per pulse, which are distributed according to a Poissonian distribution. This means most pulses actually contain no photons (no pulse is sent), some pulses contain 1 photon (which is desired) and a few pulses contain 2 or more photons. If the pulse contains more than one photon, then Eve can split off the extra photons and transmit the remaining single photon to Bob. This is the basis of the photon number splitting attack,[23] where Eve stores these extra photons in a quantum memory until Bob detects the remaining single photon and Alice reveals the encoding basis. Eve can then measure her photons in the correct basis and obtain information on the key without introducing detectable errors.
Even with the possibility of a PNS attack a secure key can still be generated, as shown in the GLLP security proof,[17] however a much higher amount of privacy amplification is needed reducing the secure key rate significantly (with PNS the rate scales as 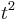 as compared to
as compared to  for a single photon sources, where
for a single photon sources, where  is the transmittance of the quantum channel).
is the transmittance of the quantum channel).
There are several solutions to this problem. The most obvious is to use a true single photon source instead of an attenuated laser. While such sources are still at a developmental stage QKD has been carried out successfully with them.[24] However as current sources operate at a low efficiency and frequency key rates and transmission distances are limited. Another solution is to modify the BB84 protocol, as is done for example in the SARG04 protocol,[25] in which the secure key rate scales as 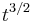 . The most promising solution is the decoy state idea,[26] in which Alice randomly sends some of her laser pulses with a lower average photon number. These decoy states can be used to detect a PNS attack, as Eve has no way to tell which pulses are signal and which decoy. Using this idea the secure key rate scales as
. The most promising solution is the decoy state idea,[26] in which Alice randomly sends some of her laser pulses with a lower average photon number. These decoy states can be used to detect a PNS attack, as Eve has no way to tell which pulses are signal and which decoy. Using this idea the secure key rate scales as  , the same as for a single photon source. This idea has been implemented successfully first at University of Toronto,[27][28] and in several follow-up QKD experiments,[29] allowing for high key rates secure against all known attacks.
, the same as for a single photon source. This idea has been implemented successfully first at University of Toronto,[27][28] and in several follow-up QKD experiments,[29] allowing for high key rates secure against all known attacks.
Hacking attacks
Hacking attacks target imperfections in the implementation of the protocol or deficiencies in the components of the physical device. If the equipment used in quantum key distribution can be tampered with, it could be made to generate keys that were not secure using a random number generator attack. Another common class of attacks is the Trojan horse attack[30] which does not require physical access to the endpoints: rather than attempt to read Alice and Bob's single photons, Mallory sends a large pulse of light back to Alice in between transmitted photons. Alice's equipment reflects some of Mallory's light, revealing the state of Alice's polarizer. This attack is easy to avoid, for example using an optical isolator to prevent light from entering Alice's system, and all other hacking attacks can similarly be defeated by modifying the implementation. Apart from Trojan horse there are several other known attacks including faked-state attacks,[31] phase remapping attacks[32] and time-shift attacks.[33] The time-shift attack has even been successfully demonstrated on a commercial quantum crypto-system.[34] This is the first successful demonstration of quantum hacking against a non-homemade quantum key distribution system. Later on, the phase-remapping attack has also been demonstrated on a commercial QKD system (made and sold by the Swiss company Id Quantique).[35]. It is one of the first successful ‘intercept-and-resend’ attacks on top of a widely used QKD implementation in commercial QKD systems. This work has been widely reported by many medias. [36][37][38][39].
In a new (and what turned out to be actually, even an earlier) claim,[40] it has now been experimentally shown that the detectors of two commercial devices could be fully remote-controlled using specially tailored bright illumination, which makes it possible to tracelessly acquire the full secret key. In a spree of publications[41][42][43] thereafter, this collaboration between the Norwegian University of Science and Technology in Norway and Max Planck Institute for the Science of Light in Germany, has now demonstrated several methods to successfully eavesdrop on commercial QKD systems based on Avalanche photodiodes (APDs) operating in gated mode.
Denial of service
Because currently a dedicated fibre optic line (or line of sight in free space) is required between the two points linked by quantum key distribution, a denial of service attack can be mounted by simply cutting or blocking the line. This is one of the motivations for the development of quantum key distribution networks, which would route communication via alternate links in case of disruption.
Weak measurement
It may be possible to measure the photons without disturbing them using Weak measurement. Fortunately such measurements can be detected because they delay the arrival of the photons slightly. However, as weak measurement becomes perfected it will be necessary for the QKD protocols to check for these time delays.
Counterfactual Quantum Key Distribution
We don't have to worry about Weak measurement or any other kind of measurement if we use a protocol developed by Tae-Gon Noh.[44] Here Alice generates a photon which randomly takes either path (a) or path (b). Path (a) stays inside Alice's secure device and path (b) goes to Bob. By rejecting the photons that he receives and only accepting the counterfactual ones that he doesn't receive, Bob can set up a secure channel that Eve can't measure. Nonetheless, Eve's attempts to read the counterfactual photons can still be detected. This protocol uses the quantum phenomenon whereby the possibility that a photon can be sent has an effect even when it isn't sent. So called Interaction-free measurement also uses this quantum effect.
History
Quantum cryptography was proposed first by Stephen Wiesner, then at Columbia University in New York, who, in the early 1970s, introduced the concept of quantum conjugate coding. His seminal paper titled "Conjugate Coding" was rejected by IEEE Information Theory but was eventually published in 1983 in SIGACT News (15:1 pp. 78–88, 1983). In this paper he showed how to store or transmit two messages by encoding them in two “conjugate observables”, such as linear and circular polarization of light, so that either, but not both, of which may be received and decoded. He illustrated his idea with a design of unforgeable bank notes. A decade later, building upon this work, Charles H. Bennett, of the IBM Thomas J. Watson Research Center, and Gilles Brassard, of the Université de Montréal, proposed a method for secure communication based on Wiesner’s “conjugate observables”. In 1990, independently and initially unaware of the earlier work, Artur Ekert, then a Ph.D. student at Wolfson College, University of Oxford, developed a different approach to quantum key distribution based on peculiar quantum correlations known as quantum entanglement.
Future
The current commercial systems are aimed mainly at governments and corporations with high security requirements. Key distribution by courier is typically used in such cases, where traditional key distribution schemes are not believed to offer enough guarantee. This has the advantage of not being intrinsically distance limited, and despite long travel times the transfer rate can be high due to the availability of large capacity portable storage devices. The major difference of quantum key distribution is the ability to detect any interception of the key, whereas with courier the key security cannot be proven or tested. QKD (Quantum Key Distribution) systems also have the advantage of being automatic, with greater reliability and lower operating costs than a secure human courier network.
Factors preventing wide adoption of quantum key distribution outside high security areas include the cost of equipment, and the lack of a demonstrated threat to existing key exchange protocols. However, with optic fibre networks already present in many countries the infrastructure is in place for a more widespread use.
See also
- Quantum Cryptography
- Quantum Computing
- Quantum Information Science
- List of quantum key distribution protocols
- Quantum network
External links
- General and Review
- Scientific American Magazine (January 2005 Issue) Best-Kept Secrets Non-technical article on quantum cryptography
- Physics World Magazine (March 2007 Issue) Non-technical article on current state and future of quantum communication
- arXiv:0802.4155 (quant-ph) February 2008 review of Quantum Cryptography
- arXiv:quant-ph/0702202v3 March 2007 review of Quantum Cryptography
- SECOQC White Paper on Quantum Key Distribution and Cryptography European project to create a large scale quantum cryptography network, includes discussion of current QKD approaches and comparison with classical cryptography
- The future of cryptography May 2003 Tomasz Grabowski
- ARDA Quantum Cryptography Roadmap
- Lectures at the Institut Henri Poincaré (slides and videos)
- Interactive quantum cryptography demonstration experiment with single photons for education
- More Specific Information
- Further Information
- Quantum Cryptography Research Groups
- Companies selling quantum devices for cryptography
- id Quantique sells Quantum Key Distribution products
- MagiQ Technologies sells quantum devices for cryptography
- QuintessenceLabs Solutions based on continuous wave lasers
- Companies with quantum cryptography research programmes
References
- ^ C. E. Shannon , Bell Syst. Tech. J. 28, 656 (1949)
- ^ H. Chau, Physical Review A 66, 60302 (2002) ([1])
- ^ C. H. Bennett, F. Bessette, G. Brassard, L. Salvail and J. Smolin "Experimental Quantum Cryptography" Journal of Cryptology vol.5, no.1, 1992, pp. 3-28.
- ^ G. Brassard and L. Salvail "Secret key reconciliation by public discussion" Advances in Cryptology: Eurocrypt 93 Proc. pp 410-23 (1993) ([2])
- ^ A. R. Dixon, Z. L. Yuan, J. F. Dynes, A. W. Sharpe, and A. J. Shields. Optics Express, Vol. 16, Issue 23, pp. 18790-18979 ([3], See also [4])
- ^ New Journal of Physics 8 193 (2006) ([5])
- ^ R. Ursin, et al. Nature Physics 3, 481 - 486 (2007) ([6])
- ^ H.-K. Lo, X. Ma and K. Chen: "Decoy State Quantum Key Distribution". Physical Review Letters 94, 230504 (See also [7])
- ^ T. Schmitt-Manderbach, et al.: "Experimental demonstration of free-space decoy-state quantum key distribution over 144 km." Physical Review Letters 98.1 010504 (2007)
- ^ http://www.technewsworld.com/story/59793.html technewsworld.com
- ^ http://www.secoqc.net/downloads/pressrelease/Banktransfer_english.pdf secoqc.net
- ^ Quantum cryptography network gets wireless link - info-tech - 07 June 2005 - New Scientist
- ^ 'Unbreakable' encryption unveiled
- ^ SwissQuantum Project Completes Longest-Running Testbed of Quantum Crytography
- ^ Tokyo QKD Network unveiled at UQCC 2010
- ^ P. W. Shor and J. Preskill, Physical Review Letters 85, 441 (2000)
- ^ a b D. Gottesman, H.-K. Lo, N. L¨utkenhaus, and J. Preskill, Quant. Inf. Comp. 4, 325 (2004)
- ^ M. N. Wegman and J. L. Carter, "New hash functions and their use in authentication and set equality, Journal of Computer and System Sciences", 22, pp 265-279, (1981)
- ^ Romain Alleaume, et al. "SECOQC White Paper on Quantum Key Distribution and Cryptography" arXiv:quant-ph/0701168v1 pp. 7 (2007) ([8])
- ^ Z. Zhang, J. Liu, D. Wang and S. Shi “Quantum direct communication with authentication” Phys. Rev. A 75, 026301 (2007)
- ^ D. Huang, Z. Chen, Y. Guo and M. Lee "Quantum Secure Direct Communication Based on Chaos with Authentication", Journal of the Physical Society of Japan Vol. 76 No. 12, 124001 (2007) ([9])
- ^ http://www.lysator.liu.se/~jc/mthesis/5_Unconditionally_secure_au.html
- ^ G. Brassard, N. Lütkenhaus, T. Mor, and B. C. Sanders. "Limitations on practical quantum cryptography." Physical Review Letters, 85(6):1330+ (2000)
- ^ P. M. Intallura, , M. B. Ward, O. Z. Karimov, Z. L. Yuan, P. See, A. J. Shields, P. Atkinson, and D. A. Ritchie, Appl. 43 Phys. Lett. 91, 161103 (2007)
- ^ V. Scarani, A. Ac´ın, G. Ribordy and N. Gisin, Phys. Rev. Lett. 92, 057901 (2004)
- ^ W.-Y. Hwang, Phys. Rev. Lett. 91, 057901 (2003)
- ^ Y.Zhao, B. Qi, X. Ma, H.-K. Lo, and L. Qian, Phys. Rev. Lett., 96, 070502 (2006).
- ^ Y.Zhao, B. Qi, X. Ma, H.-K. Lo, and L. Qian, in Proc. IEEE ISIT, pp. 2094--2098 (2006).
- ^ Z. L. Yuan, A. W. Sharpe, and A. J. Shields, Appl. Phys. Lett. 90, 011118 (2007)
- ^ Vakhitov, A. V. Makarov and D. R. Hjelme, J. Mod. Opt. 48, 2023 (2001)
- ^ V. Makarov and D. R. Hjelme, J. Mod. Opt. 52, 691. (2005)
- ^ C.-H. F. Fung, B. Qi, K. Tamaki, and H.-K. Lo, Phys. Rev. A 75, 032314. (2007)
- ^ B. Qi, C.-H. F. Fung, H.-K. Lo, and X. Ma, Quant. Info. Compu. 7, 43 (2007)
- ^ Y. Zhao, C.-H. F. Fung, B. Qi, C. Chen, and H.-K. Lo, Phys. Rev. A 78:042333 (2008)
- ^ F. Xu, B. Qi, and H.-K. Lo, New J. Phys. 12, 113026 (2010)
- ^ Quantum crypto boffins in successful backdoor sniff - Erroneous error-handling undermines bulletproofness retrieved 2010-05-26
- ^ http://www.nature.com/news/2010/100520/full/news.2010.256.html
- ^ http://www.economist.com/node/16681905
- ^ http://physicsworld.com/cws/article/news/42667
- ^ L. Lydersen, C. Wiechers, C. Wittmann, D. Elser, J. Skaar and V. Makarov, Nat. Photonics 4, 686 (2010)
- ^ L. Lydersen, C. Wiechers, C. Wittmann, D. Elser, J. Skaar and V. Makarov, Opt. Exp. 18, 27938 (2010)
- ^ C. Wiechers, L. Lydersen, C.Wittmann, D. Elser, J. Skaar, Ch. Marquardt, V. Makarov and G. Leuchs, New J. Phys. 13, 013043 (2011)
- ^ N. Jain, C. Wittmann, L. Lydersen, C. Wiechers, D. Elser, Ch. Marquardt, V. Makarov and G. Leuchs, arXiv:1103.2327 (2011)
- ^ Tae-Gon Noh, Counterfactual Quantum Cryptography, Physical Review Letters, 103, Issue 23, 230501 (2009).
|
|||||||||||||||||||||||||||||||||||